Euclid
|
A new but possibly entertaining productivity sink? http://euclidthegame.com
Robert C ============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
I have to confess I got stuck at Level 23 because, I'm claiming, I
wasn't familiar with the geometry of homothetic
centers. Is there a complexity site that does the same sort
of thing? It looks like a great way to extend one's education on an
otherwise relatively difficult subject.
Robert C On 2/27/15 2:54 PM, Robert J.
Cordingley wrote:
A new but possibly entertaining productivity sink? http://euclidthegame.com ============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
I am also stuck at 23, but I'm not sure
it is from lack of success...
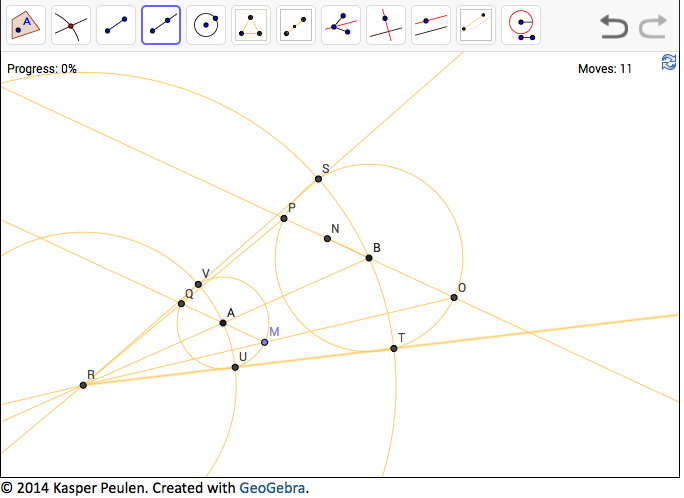
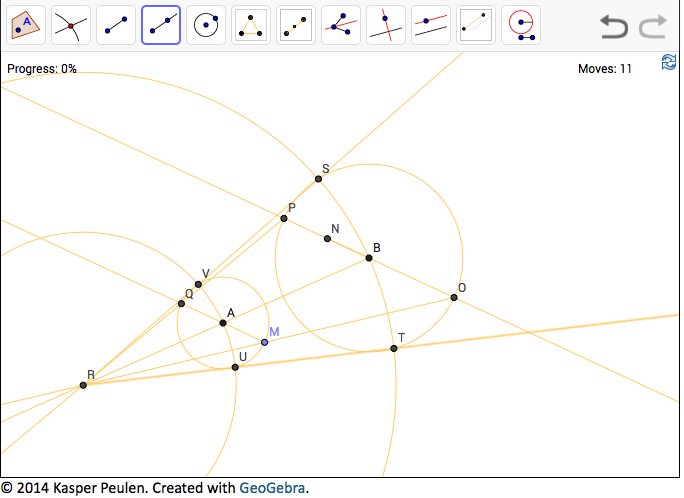
RVS and RUT "should" match the criteria (using your homothetic centers "R" hint). 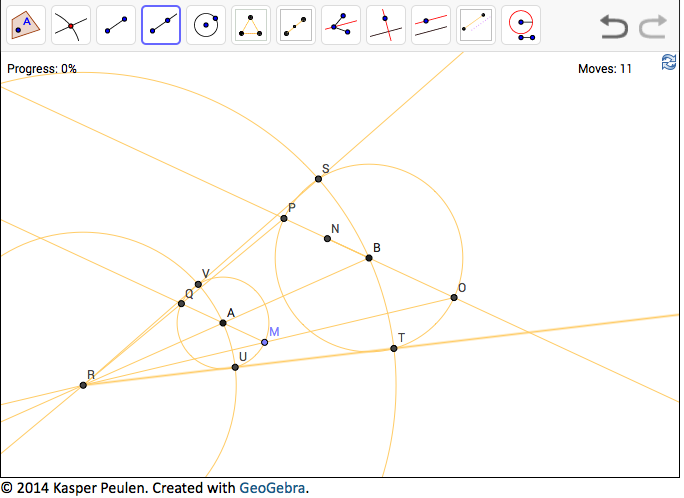 I had at least one other approach which *also* failed to "pass". I'm a little unclear on how the "snap to grid" and/or "snap to intersection" works, which *might* be bolloxing things up? I'm wondering if *anyone* else took your bait? I ripped through these "pretty fast" stumbling on 16 I think for a little extra time. I have to confess I got stuck at Level 23 because, I'm claiming, I wasn't familiar with the geometry of homothetic centers. Is there a complexity site that does the same sort of thing? It looks like a great way to extend one's education on an otherwise relatively difficult subject. ============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
I finally "punted" by hand-entering the
implied URL for problem 24 and using your hint of homothetic
centers, found a similar solution forthwith, but alas, the program
still does not seem to recognize it as a solution.... hmmm? 25
(pentagram inscribed into a circle) was an interesting challenge
and again, my solution was not acknowledged by the system
either... "sigh"!
============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
In reply to this post by Steve Smith
Hi Robert, Steve, One way to arrive at a solution is to make a third circle with radius r2 - r1 (https://en.wikipedia.org/wiki/Tangent_lines_to_circles). This reduces the problem to finding a tangent to a point outside of the new circle (https://en.wikipedia.org/wiki/Thales%27_theorem, bottom figure for instance). Since the tangent is invariant to this type of transformation, you can scale your solution to the original circles. Interesting game; thanks for posting. Best, Shawn On Sun, Mar 1, 2015 at 11:43 PM, Steve Smith <[hidden email]> wrote:
============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
In reply to this post by Steve Smith
Hi Robert, Steve, One way to arrive at a solution is to make a third circle with radius r2 - r1 (https://en.wikipedia.org/wiki/Tangent_lines_to_circles, under external tangents). This reduces the problem to finding a tangent to a point outside of the new circle (https://en.wikipedia.org/wiki/Thales%27_theorem, bottom figure for instance). Since the tangent is invariant to this type of transformation, you can scale your solution to the original circles. Interesting game; thanks for posting. Shawn On Sun, Mar 1, 2015 at 11:43 PM, Steve Smith <[hidden email]> wrote:
============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
Shawn -
Good to hear from you stranger! I'm pretty confident in my solution, I'm not sure why the program doesn't acknowledge it. Do you (or anyone) see any problem with it? The method was
steps 4 and 5 could delete one of the two substeps as
redundant. not sure how GeoGebra actually determines a match with their
own "solution".
============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
|
Dont forget to Euclid your work to show got to the answers for full credit. :P (Rimshot)On Fri, Mar 6, 2015 at 9:33 AM, Steve Smith <[hidden email]> wrote:
============================================================ FRIAM Applied Complexity Group listserv Meets Fridays 9a-11:30 at cafe at St. John's College to unsubscribe http://redfish.com/mailman/listinfo/friam_redfish.com |
«
Return to Friam
|
1 view|%1 views
| Free forum by Nabble | Edit this page |